Intro.
8-2장에서 합성곱 신경망으로 Fasion MNIST 이미지를 분류하는 모델을 만들어봤다.
이번 장에서는 합성곱 층이 이미지에서 대체 무엇을 학습한 건지 보기 위해 가중치와 특성 맵을 시각화해보자!
또, 그냥 Sequential 클래스만 쓰는 게 아니라 함수형 API를 써서 좀 더 복잡한 모델을 만들어보자!
1. 가중치 시각화
필터와 특성맵의 관계
- 합성곱 층은 여러 개의 필터로 이미지의 특징을 학습함 → 필터에는 가중치 & 절편이 담겨있음 → 여기서 가중치는 입력 이미지의 어떤 특징을 두드러지게 표현하는 역할을 함! (절편은 시각적 의미 X)
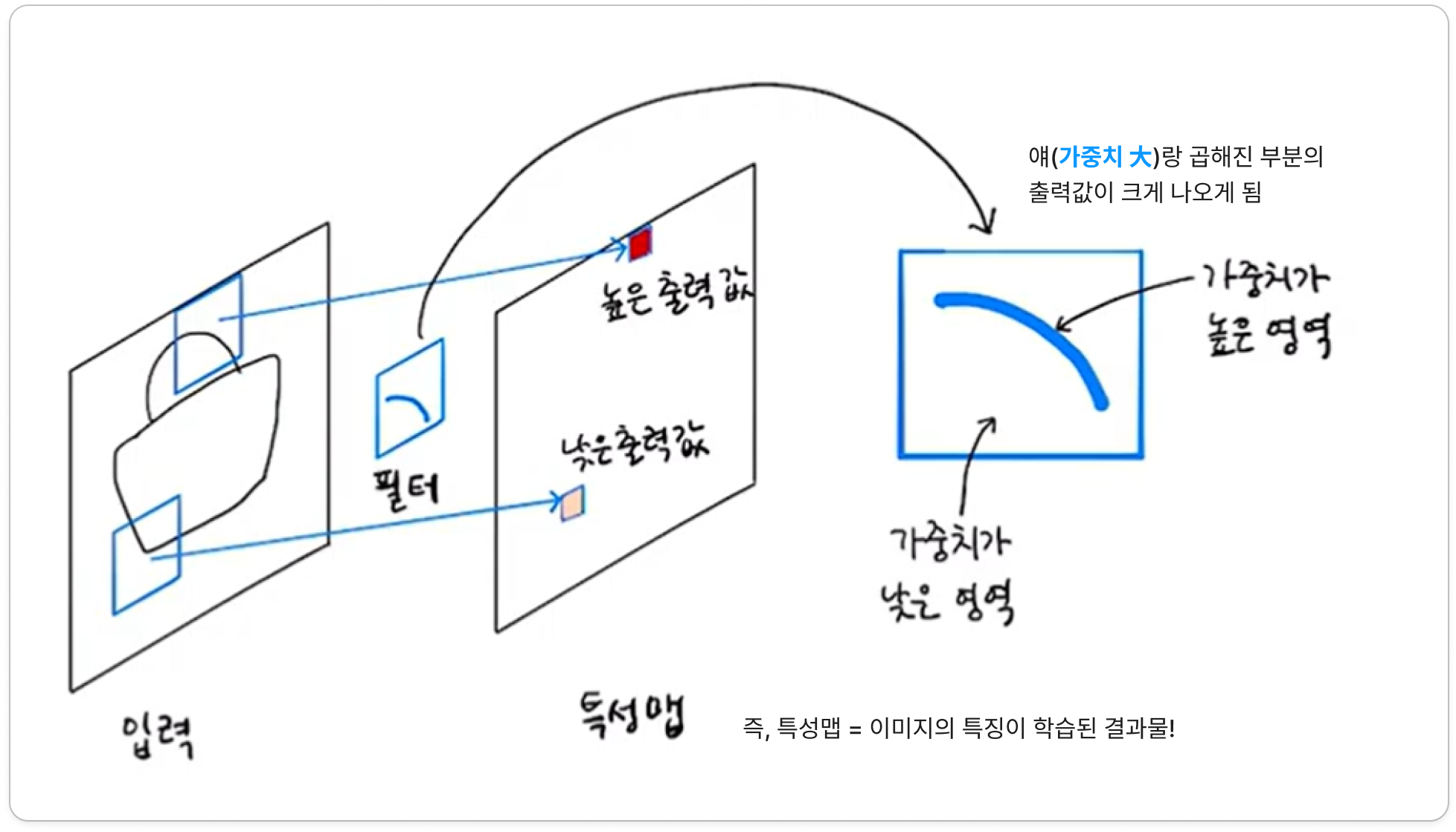
- ex) 가방 이미지에 아래와 같은 필터가 합성곱 연산을 수행하면, 손잡이가 있는 쪽 픽셀들과 곱해졌을 때 높은 출력값이 나옴
- ➡️즉, 필터의 패턴(가중치 높은 부분들이 이루는 모양)을 잘 반영하고 있는 곳은 출력값 大, 다른 모양을 띠는 곳은 출력값 小
Conv2D 학습 전후 가중치 비교
- 우리가 8-2장에서 만들었던 모델로 확인해보자 = `load_model` 써서 그대로 가져옴
- `.layers` 로 층 구조를 출력해보면, 우리가 만든 구조가 그대로 담겨있음을 확인 가능!
- Conv2D - MaxPooling2D - Conv2D - MaxPooling2D - Flatten - Dense - Dropout - Dense
- 이 중에 첫 번째 Conv2D 층의 가중치를 조사해보자!

첫 번째 Conv2D 층의 학습 후 가중치
- 층의 가중치 & 절편은 `.weights` 속성에 저장되어 있음 ⇒ 그 리스트의 0번째 원소가 가중치, 1번째 원소가 절편!
- 가중치 : 깊이가 1인 (3,3) 필터를 32개 사용했으므로 `(3,3,1,32)` / 절편 : 필터마다 1개씩 총 32개니까 `(32,)`

- ① 이 가중치 배열(tensor)의 평균과 표준편차를 계산해봄 ⇒ Numpy 배열로 변환 후 `mean()`, `std()`으로 계산
- ex) 평균 -0.024 / 표준편차 0.249
- ② 가중치들이 주로 어떤 값을 갖고 있는지 분포(histogram) 그려봄 ⇒ `reshape`로 1차원으로 펼치고 `plt.hist`로 시각화
- ex) 총 288 (=3*3*1*32) 개의 가중치 값이 분포로 그려짐

- ③ 이번엔 32개의 필터(가중치 배열)를 3*3 이미지로 출력해봄
- `imshow` : 입력받은 배열의 최대/최소값으로 픽셀의 강도를 표현함. (ex. 값이 1이든 0.1이든, '그 배열에서' 최대값이면 밝은 노란색, 최소값이면 어두운 색) ⇒ 서로 다른 배열끼리 비교하기 위해 `vmin`, `vmax`로 픽셀 강도를 나타낼 절대값을 지정해줌!
- 결과를 보면, 가중치마다 어떤 패턴이 있음 (ex. 마지막 필터의 경우, 세로 직선이 있는 픽셀을 만나면 크게 활성화될 거임!)

첫 번째 Conv2D 층의 학습 전 가중치
- 그냥 `Sequential` 객체 만들고, 동일한 설정으로 Conv2D 층을 `.add`
- 그리고 똑같이 `.layers`에 접근해서 가중치 배열 가져옴

- ① 마찬가지로 가중치 배열의 평균과 표준편차를 계산해봄
- ex) 평균 0.005 / 표준편차 0.081 (🆚학습 후: 평균 -0.024 / 표준편차 0.249)
- 평균은 비슷하게 0에 가까운데, 표준편차가 훨씬 작음!
- ② 마찬가지로 분포(histogram) 그려봄
- 대부분의 가중치가 -0.1 ~ 0.1 사이에 있고, 비교적 고른 분포 ➡️ tensorflow는 신경망의 가중치를 초기화할 때 균등분포에서 랜덤하게 설정하기 때문!

- ③ 마찬가지로 필터를 3*3 이미지로 출력해 봄
- 특별히 활성화된(밝은) 곳이 없이 밋밋한 모습 = 초기화 상태!

➡️①,②,③ 비교 결과를 종합해보니, Conv2D 층이 이미지 분류 정확도를 높이기 위해 유용한 패턴을 학습했다는 것을 알 수 있음!
2. 함수형 API
- 👨🏫특성맵 시각화 해보기 전에 함수형 api에 대한 내용을 짚고 넘어갑시다
- 그동안 사용한 `Sequential` 클래스는 층을 차례대로 쌓아서 모델을 구성함
- 그런데 좀 더 복잡한 모델(ex. 입력이나 출력이 2개 이상인 경우)을 만들 땐 사용하기 어려움
- 이럴 때 '함수형 API(functional API)'를 사용할 수 있음!
- keras는 모델 클래스를 함수처럼 사용할 수 있는 기능을 제공함
= 모델 객체에 직접 input을 넣고 output을 받을 수 있음
= input, output 연쇄적으로 조합해서 복잡한 모델 만들기에 훨씬 용이함! - ⭐`Model()` 클래스에 입력과 최종 출력을 지정하면 모델 완성!
- 대신 Sequential api와 달리, 제일 첫 InputLayer를 직접 만들어서 넣어줘야 함! (`keras.Input` 함수에 입력 크기를 지정해서 만들 수 있음. 아래 그림의 ② 참고)
- keras는 모델 클래스를 함수처럼 사용할 수 있는 기능을 제공함
- Ex) Dense층 2개짜리 모델을 만드는 경우
- 원래는 ①처럼 Dense층 객체를 만들고, `.add()`로 Sequential 객체에 전달해서 쌓는 방식이었음
- 근데 그게 아니라, ②처럼 Dense층 객체를 아예 함수처럼 호출할 수도 있음!

➡️이 함수형 API를 사용하면 중간의 일부 층만 떼어내서 시각화가 가능함!!
- ex) 어떤 이미지를 넣었을 때, 첫 번째 Conv2D까지만 통과한 출력(특성 맵)을 얻고 싶음
- 함수형 API로 `Model(<첫 입력>, <Conv2D의 출력>)` 객체를 만들어서 쓰면 됨!
- <첫 입력> : 모델의 `inputs` 속성으로 참조 가능
- <Conv2D의 출력> : 해당 층의 `output` 속성으로 참조 가능


3. 특성맵 시각화
첫 번째 합성곱 층
- 이제 이미지 샘플 1개를 방금 만든 `conv_acti`에 넣어서, 첫 번째 Conv2d 통과한 특성맵을 시각화해보자!
- 0번째 샘플 선택 (배치 차원 유지하기 위해 슬라이싱 사용. 8-2장 'Hmmmm...' 참고)
- (28,28) 크기를 (28,28,1) 차원으로 전처리 (8-2장 전처리와 동일)
- ` conv_acti .predict()`로 이 샘플에 대한 예측(분류) 수행
- ➡️필터 32개 썼으므로 출력(특성맵)도 32개 나옴!

- 이 32개의 특성맵을 각각 2차원 이미지로 출력해보자! (Matplotlib의 `imshow()` 함수 사용)
- (1) 세로선을 감지하는 필터로 보임 >>> 실제로 특성맵의 세로선 부분이 강하게 활성화됨
- (2) 가중치가 전반적으로 다 큰 필터 >>> 원래 이미지의 전면이 활성화됨
- (3) 가중치가 전반적으로 다 작은(음수) 필터 >>> 큰 양수는 큰 음수가 되고 작은 양수는 작은 음수가 되니까, 0에 가까운 작은 양수들이 있던 배경 부분이 상대적으로 활성화됨

두 번째 합성곱 층
- 같은 방식으로, 두 번째 Conv2d 통과한 특성맵도 시각화해보자!
- 아까 그 `Model(<첫 입력>, <Conv2D의 출력>)` 객체에서 뒷부분만 바꿔주면 됨

- 2번째 Conv2d 층에서는 필터 64개 사용했음 ⇒ 64개의 특성맵들을 각각 2차원 이미지로 출력해보자
- 하지만 이제는 어떤 부위를 감지하는지 직관적으로 이해하기 어려움😂 = "Black Box"
(14,14,32) 특성맵에 (3,3,32) 필터를 곱했으니 값이 복잡해지는 게 어쩌면 당연한,,, - 이런 현상은 Conv층을 많이 쌓을수록 심해짐... (👨🏫이를 바꿔 생각하면, 초반의 합성곱층은 시각적인 정보를 감지하고, 후반의 합성곱층은 추상적인 정보를 학습한다고 볼 수도 있겠죠)
- 하지만 이제는 어떤 부위를 감지하는지 직관적으로 이해하기 어려움😂 = "Black Box"

🤔 Hmmmm...
keras 3.x 버전에서 업데이트된 내용들 체크 필요할 듯 (25년 2월 기준)
1) 모델 저장 방식
- 모델 가중치+구조까지 통째로 저장하는 save() 메소드는 .keras 확장자를 가진 파일에 압축하여 저장함
(ex: `model.save('model-whole.keras')` )
- 🆚가중치만 저장하는 save_weights()는 그대로 .h5 확장자 사용
(ex. `model.save_weights('model.weights.h5')` )
2) input 속성
- 모델(층)이 호출되기 전에는 input 속성이 정의되지 않음. 그래서 `model.inputs` 속성을 사용함.
🤓 To wrap up...
'ML & DL > 머신러닝 기초' 카테고리의 다른 글
| [혼자 공부하는 머신러닝+딥러닝] 8-2. 합성곱 신경망을 사용한 이미지 분류 (0) | 2025.03.11 |
|---|---|
| [혼자 공부하는 머신러닝+딥러닝] 8-1. 합성곱 신경망의 구성요소 (1) | 2025.03.10 |
| [혼자 공부하는 머신러닝+딥러닝] 🎊혼공학습단 완주 회고록🎊 (0) | 2025.03.07 |
| [혼자 공부하는 머신러닝+딥러닝] 7-3. 신경망 모델 훈련 (0) | 2025.03.07 |
| [혼자 공부하는 머신러닝+딥러닝] 7-2. 심층 신경망 (1) | 2025.02.28 |
