데이터마이닝에 관한 스터디를 진행하고자 정리한 내용입니다. 참고한 자료들은 아래에 따로 정리해두었으며,개인 공부 과정에서 틀린 부분이 있을 수 있습니다. (잘못된 부분은 알려주시면 수정하겠습니다!)
Intro.
이번 시간에는 지도학습의 대표적인 알고리즘 중 하나인 의사 결정 나무(Decision Tree)에 대해 다룹니다. 단순해보일 수 있지만 강력한 성능의 앙상블 모델(XGBoost, LightGBM 등)의 기반이 되는 중요한 알고리즘입니다.
1. Decision Tree 소개
1.1. 기본 아이디어
- 의사결정나무(Decision Tree)는 간단한 규칙들을 논리적으로 결합한 순차적 모델(sequential model)로, 흔히 아는 스무고개와 비슷한 매커니즘이라고 이해하면 편합니다. 데이터를 잘 나눌 수 있는 질문(규칙)들을 찾아나가는 과정이, 나무가 가지를 뻗어나가는 과정과 흡사하여 Tree라는 이름이 붙었습니다.

- 빠른 이해를 위해 예시를 함께 봅시다. 오른쪽 그림은 타이타닉 프로젝트를 의사결정나무로 구현한 모습입니다. (*타이타닉 프로젝트란, 타이타닉 탑승자들의 정보 (나이, 성별, 동행자 수 등)를 바탕으로 생존 여부를 예측하는 데이터 분석 프로젝트입니다.)
- 위의 트리 모델을 통해 탑승자의 생존 여부를 예측하는 과정을 따라가봅시다. 가장 먼저, “남자인가?”라는 성별에 대한 질문을 만날 것입니다. 그러면 대답에 따라 영역이 분할되는데, “아니오”를 선택한 경우 생존한다고 예측하지만 “예”를 선택한 경우 아래의 추가 질문이 이어집니다. 이어서 ‘나이’에 대한 질문이 나오고, “예”라고 대답하면 사망, “아니오”라고 대답하면 또 다음 질문으로 내려가게 됩니다.
- 이처럼 Decision Tree는 일련의 질문(규칙)과 그에 따른 대답으로 예측값이 정해지게 되는 알고리즘인데요. 이러한 과정은 “순차적으로 독립변수의 공간을 분할한다”고도 표현할 수 있습니다.
- 만약 아래와 같이 분기된 트리(ex. 야구선수의 연봉을 예측하는 모델)가 있다면, 이를 오른쪽처럼 2차원 평면에 나타낼 수 있습니다. 2개의 독립변수(Years, Hits)에 따라 관측값의 영역이 분할된 것이죠.
- 이렇게 독립변수(X)들이 차지하고 있는 공간을 질문(규칙)에 따라 분할해나가고, 그렇게 분할된 공간에 적절한 결론을 내려주는 것이 Decision Tree 알고리즘의 핵심입니다.
1.2. 용어 정리
- 의사결정나무를 비롯한 트리 기반 모델에서 주요하게 쓰이는 용어들을 정리해보았습니다.
- Parent node(부모 노드) : 분기 이전의 상위 노드
- Child node(자식 노드) : 분기 이후의 하위 노드
- Root node(루트 노드) : 전체 관측값을 포함하는 최상위 노드. 부모 노드가 없음.
- Internal node(내부 노드) : 부모 노드와 자식 노드가 모두 있는 노드
- Leaf node(리프 노드) : 분기가 끝난 최종 노드. 자식 노드가 없음. (=Terminal node라고도 함)
- Depth(깊이) : 루트 노드부터 연결된 노드의 개수 (루트 노드 본인은 제외)
- Split criterion(분기 기준) : 노드를 분할하는 기준 (ex. Gini index, Entropy 등)

- Decision Tree는 모델 학습이 끝나면 Leaf node에 결과값이 들어가게 되는데, 이때 그 결과값은 문제의 성격에 따라 달라집니다. (아래에서 더 자세히 다루게 됩니다)
- 회귀 문제인 경우에는 ‘노드 내 관측값의 평균’을 결과로 반환합니다.
- 분류 문제인 경우에는 ‘노드 내 관측값의 최다 클래스’를 결과로 반환합니다.
1.3. 의사결정나무 종류
- Decison Tree를 기반으로 한 알고리즘은 여러 종류가 있습니다. 그 중에도 대표적으로 ID3, C4.5, CART가 있는데, 각각의 차이점을 간단히 살펴보겠습니다. (구체적인 작동 원리는 2~4절에 설명되어있습니다. 개념을 처음 접하시는 분들은 아래 내용을 먼저 보고 오시면 이해가 더욱 쉬울 것 같습니다)
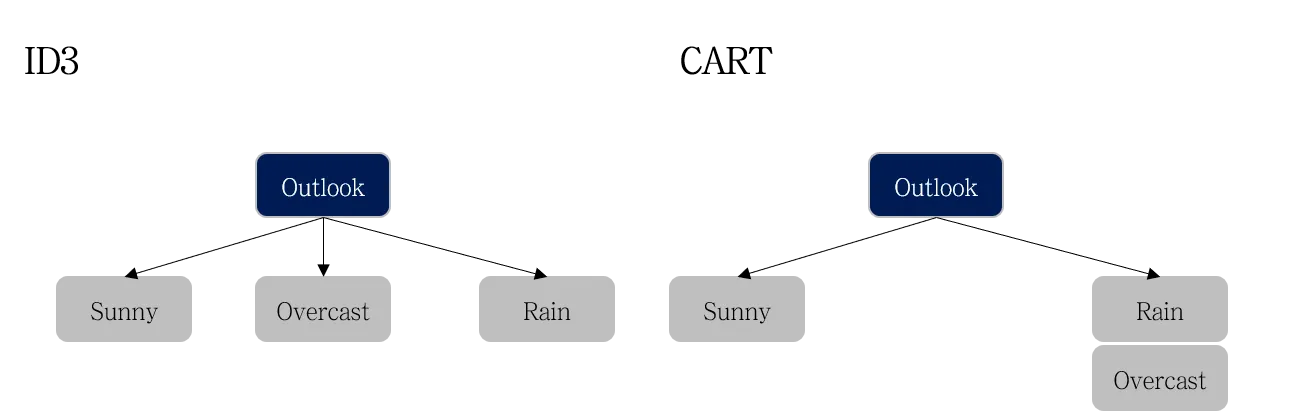
① ID3 (Iterative Dichotomiser 3)
- 기본 개념 :
- Ross Quinlan(1986)이 개발한 알고리즘.
- 정보이득(Information Gain)을 기준으로 노드를 분할하며, 엔트로피(Entropy)를 기준으로 Information Gain 계산함.
- 분기 방식 : 한 노드에 대해 여러 갈래로 분기할 수 있음 (다지 분리)
- 독립 변수 : 범주형만 지원함 (연속형 변수를 사용하려면 사전에 범주형으로 변환해야 함)
- 문제 유형 : 분류 문제만 적용 가능
- 한계점 :
- 과적합(overfitting) 가능성이 높음
- 결측값을 직접 처리하는 기능이 없음.
② C4.5
- 기본 개념:
- Ross Quinlan(1993)이 ID3의 단점을 보완한 알고리즘.
- 정보이득(Information Gain)이 아닌 정보이득비(Information Gain Ratio)를 사용하여 과적합을 방지함.
- 분기 방식 : 한 노드에 대해 여러 갈래로 분기할 수 있음 (다지 분리)
- 독립 변수 : 범주형, 연속형 모두 지원함
- 문제 유형 : 분류 문제만 적용 가능
- 장점 :
- 연속형 변수 처리 가능 (데이터를 특정 값 기준으로 이진 분할)
- 결측값 처리 기능 포함
- 가지치기 기능 포함
- 한계점 :
- 분할 과정이 ID3보다 복잡하여 계산량이 많음
- 분할 기준이 균형이 맞지 않을 경우 성능 저하 가능
③ CART (Classification and Regression Tree)
- 기본 개념:
- Breiman et al. (1984)이 개발 알고리즘.
- 이진 분할(binary split) 방식을 사용하며, 회귀는 MSE 또는 MAE, 분류는 Gini 불순도를 사용함
- 👍실제 구현에서 가장 많이 쓰이며, Random Forest, Gradient Boosting 등에서 기본 트리 모델로 활용됨
- 분기 방식 : 한 노드에 대해 두 갈래로만 분기할 수 있음 (이지 분리)
- 독립 변수 : 범주형, 연속형 모두 지원함
- 문제 유형 : 분류, 회귀 문제 모두 적용 가능
- 장점 :
- 회귀 문제도 처리 가능
- 한계점 :
- 이진 분할로만 이루어져 C4.5보다 유연성이 낮음
- ※ 실제 파이썬에서 DecisionTreeClassifier를 사용할 때는 범주형 변수를 직접 사용할 순 없음 (플러스알파 참고)

살펴본 의사결정나무 종류를 표로 정리해보면 위와 같습니다. 그럼 이제 의사결정나무 알고리즘이 어떤 과정을 통해 학습되는지 살펴보겠습니다. (설명의 기준은 가장 일반적으로 쓰이는 CART를 기준으로 합니다.) 학습 매커니즘의 Key idea를 요약하면 아래와 같습니다.
🔑Key Ideas in Decision Tree (트리 알고리즘의 핵심이 되는 2가지 질문)
1. 어떻게 분기할 것인가?
▶ 1회성 분기가 아니라, 반복적으로 분기하자! = 재귀적 분기(Recursive Partitioning)
▶ “잘” 분기하자! = 정보이득이 커지는 방향으로 분기 (분류는 불순도가 낮아지게! 회귀는 RSS가 작아지게!)
2. 어디까지 분기할 것인가?
▶ 과적합 되기 전까지만 분기하자! = 사전 가지치기 (pre-pruning)
▶ 끝까지 분기한 뒤, 다시 적당히 합치자! = 사후 가지치기 (post-pruning)
2. DecisionTree Classifier
먼저 Decision Tree를 분류 문제에 적용한 DecisionTreeClassifier에 대해 알아보도록 하겠습니다.
2.1. 분기 기준 : Impurity
- DecisionTreeClassifier는 영역(노드)들의 불순도가 낮아지는 방향으로 분기합니다.
- 불순도(impurity)란, 분기된 영역 내에서 서로 다른 범주의 샘플들이 얼마나 포함되어 있는가를 의미합니다. 쉽게 말하면 ‘다양한 클래스(범주)가 섞여 있는 정도’라고 할 수 있고, 따라서 이 불순도가 높을수록 분류가 잘 되지 않았다고 판단할 수 있습니다.
- 불순도를 측정하는 방법으로는 Misclassification Rate, Gini Index, Entropy 등이 여러가지가 존재합니다. (CART는 Gini Index, ID3는 Entropy를 사용함)
- 분기했을 때 불순도가 감소하는 양을 “정보 이득(Information Gain)”이라고 함 = 정보 이득이 커지는 방향으로 분기함!
① Gini Index(지니 계수)
- 영역 내에서 임의로 뽑은 두 개의 샘플이 서로 다른 클래스일 확률을 기반으로 계산되며, 계산 식은 다음과 같음
- $m$은 전체 클래스 개수, $p_k$는 클래스k가 등장할 확률 (=클래스k의 비율)

- 불순도 & 정보이득 계산 예시
- A는 분기 전 영역, B는 분기 후 영역이며, 분기 후 영역의 불순도는 영역들의 불순도를 가중합하여 계산함
- 이렇게 분할한 경우, 정보이득 = 0.46875 − 0.34375 = 0.125가 되는 것!

② Entropy(엔트로피)
- 영역(노드)이 얼마나 예측하기 어려운 상태인지 나타내는 지표로, 계산 식은 아래와 같음
- log는 정보량을 측정하기 위해 사용됨 (➕플러스알파 참고)
- 엔트로피는 원래 정보 이론(Information Theory)에서 유래한 개념임. 만약 어떤 그룹이 완전히 한 가지 클래스로만 이루어져 있다면, 예측이 쉬우니까 엔트로피가 낮음. 반면 여러 클래스가 섞여있으면 예측이 어려우니까 엔트로피가 커짐.

- 불순도 & 정보이득 계산 예시
- A는 분기 전 영역, B는 분기 후 영역이며, 분기 후 영역의 불순도는 영역들의 불순도를 가중합하여 계산함
- 이렇게 분할한 경우, 정보이득 = 0.955 − 0.6445 = 0.3105가 되는 것!

2.2. 학습 프로세스
예시 상황 : 24개 가구에 대해서 잔디깎이 기계가 있는지 여부를 분류하려고 한다. 독립변수로는 수입(Income)과 마당 크기(Lot size)를 사용했다. 전체 24개 가구 중 12개 가구는 잔디깎이를 소유(Owner) 중이고, 12개 가구는 소유하지 않고 있다.(Non-owner)
① 한 변수를 기준으로 관측값을 정렬한다.
- ex) Lot size 기준 오름차순 정렬

② Split 가능한 모든 경우의 불순도를 탐색한다.
- ex) 첫 번째 Split 후보의 IG(정보이득)은 아래와 같이 계산된다.
- ⭐변수가 여러 개일 경우, 각 변수에 맞게 정렬해가며 전부 탐색한다. (ex. Income 기준으로도 정렬해서 불순도 탐색)

③ 탐색한 모든 경우 중에 가장 IG가 큰 경우에 따라 분기한다
- 이렇게 모든 경우를 탐색해 최선의 결과를 찾으려는 알고리즘을 ‘탐욕적(greedy) 알고리즘’이라고 부른다.
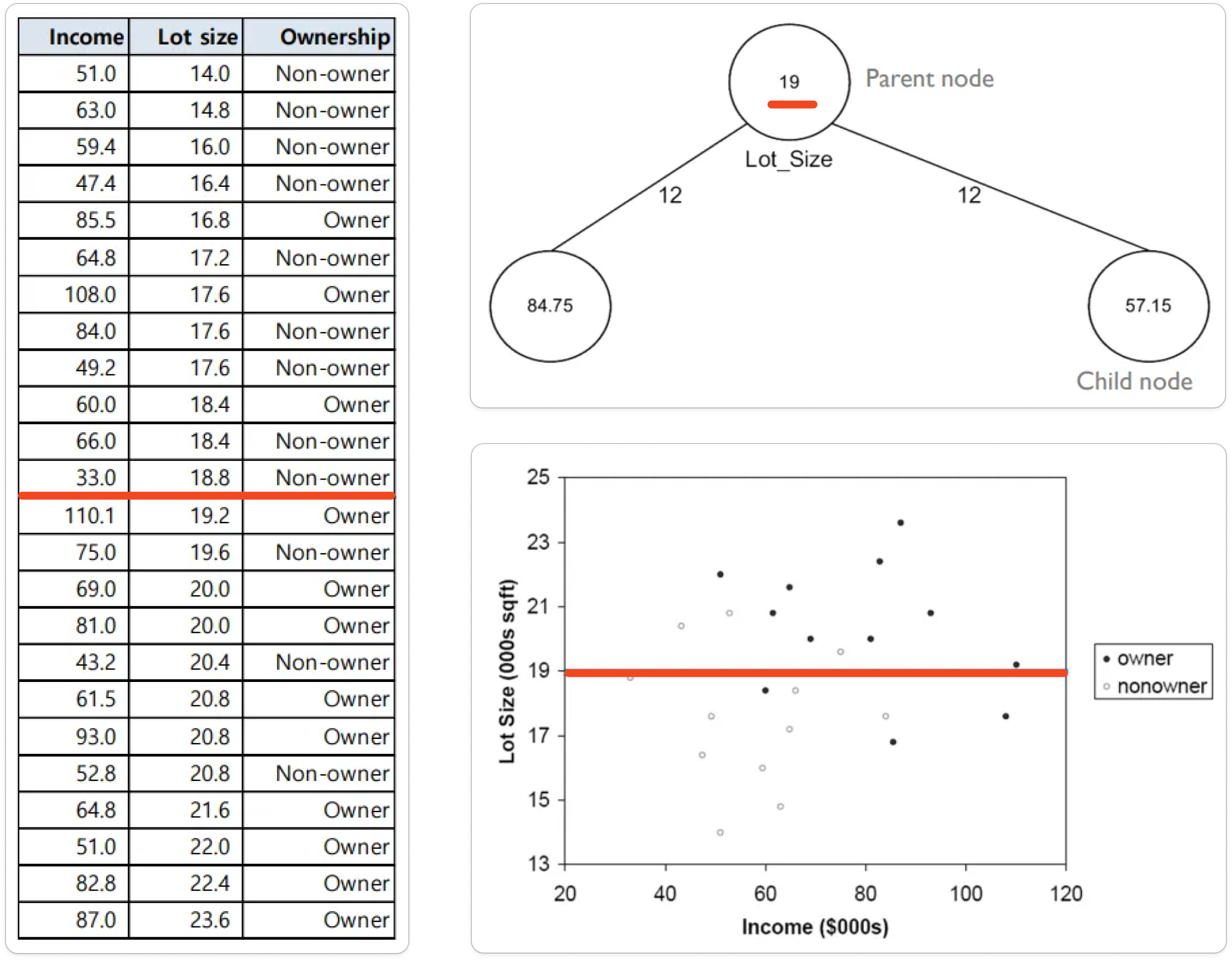
④ 분기되는 노드를 따라 내려가면서, 위 과정을 반복한다.
- 이 과정이 곧 독립변수의 공간을 분할하는 것! (지금은 변수가 2개라 2차원으로 그렸지만 변수가 많아지면 n차원 공간을 쪼개나가게 된다)

⑤ Information Gain=0 이 되면 분기를 종료한다.
- 서로 다른 클래스의 관측값이 완전히 겹쳐있지 않은 이상, 학습 데이터를 100% 구분할 수 있다.
- 이렇게 완전히 구분될 때까지 분기한 최종 트리를 Full-Tree라고 한다. (아래 그림에 보이다시피, Full-Tree는 모든 구역의 불순도가 0이 됨)

⑥ 이렇게 트리가 완성(학습)되고 나면, 새로운 객체는 만들어둔 트리를 따라 내려가서 Leaf node의 비율대로 판단하면 된다.
3. DecisionTree Regressor
이번엔 Decision Tree를 회귀 문제에 적용할 수 있게 변형시킨 DecisionTreeRegressor에 대해 알아봅시다. 기본적인 알고리즘 컨셉은 동일하지만, 분기하는 기준이 달라집니다.
3.1. 분기 기준 : RSS
- DecisionTreeRegressor는 영역(노드) 내 Residual Sum of Squares를 최소화하는 방향으로 분기합니다.
- 잔차제곱합(RSS)는 각 샘플의 실제 값과 예측 값(노드의 평균) 간의 차이를 제곱하여 합산한 값입니다. (➕일반적으로 회귀 모델에서 사용하는 비용함수 MSE는 바로 이 RSS를 자유도로 나눠준 값! 플러스알파 참고.)
- $y_i$는 실제값, $\hat{y}$는 예측값, n는 샘플 개수

3.2. 학습 프로세스
예시 상황 : 어느식당에서 손님들의 정보를 바탕으로 리뷰 평점을 예측하려고 한다. 독립변수로는 지불 금액(Price), 주차 비용(Parking fee), 외국인 여부(Foreign)를 사용했다.
① 한 변수를 기준으로 관측값을 정렬한다.
- ex. Price를 기준으로 오름차순 정렬

② Split 가능한 모든 경우의 RSS를 탐색한다.
- ex) ‘Price ≤ 13.0’을 기준으로 Split한 경우, RSS 값은 아래와 같이 계산된다.
- ⭐(분류와 마찬가지로) 모든 독립변수마다 RSS가 최소가 되는 지점을 탐색한다.

③ 탐색한 모든 경우 중에 가장 RSS가 작은 경우에 따라 분기한다.
- ex) 세 변수 각각을 기준으로 했을 때 RSS가 [ 6412.4 , 3961.8 , 11685.0] 이므로, 첫 번째 분기 기준은 `Parking fee≤ 7.75`로 채택!

④ 분기되는 노드를 따라 내려가면서, 위 과정을 반복한다.
⑤ RSS 값이 더이상 작아지지 않으면 분기를 종료한다.

⑥ 이렇게 트리가 완성(학습)되고 나면, 새로운 객체는 만들어둔 트리를 따라 내려가서 Leaf node의 예측값(평균값)대로 판단하면 된다.
➕플러스 알파
① DecisionTreeClassifier에서 범주형 변수 사용하는 방법
- CART는 데이터를 두 갈래로 분할(Binary Split)하므로 연속형 변수는 특정 임곗값(threshold) 기준으로 나눌 수 있습니다. 그런데 데이터가 범주형이면 분할 과정에서 크기 비교(<=, > 등)를 수행할 수가 없죠.
- 예를 들어, 독립변수에 " Color"라는 범주형 변수가 있다고 합시다. (Color: [Red, Blue, Green, Yellow]) 이때는 "Red, Blue" vs "Green, Yellow"로 나눌 수도 있고, "Red" vs "Blue, Green, Yellow"로 나눌 수도 있고.. 선택지가 너무 많아져서 최적의 분할을 찾기 어려워집니다.
- 그래서, Scikit-Learn에서 DecisionTreeClassifier를 사용하려면 범주형 변수를 반드시 수치형으로 변환해야 합니다.
- 변환 방법 ① Label Encoding
- 각 범주를 정수로 변환하는 방법으로, 위 예시의 경우 Red=0, Blue=1, Green=2..와 같이 변환할 수 있습니다.
- 하지만 이 정수들이 크기의 의미를 갖기 때문에 순서형(ordinal) 데이터에 적합하고, 위 예시의 '색상'처럼 순서 의미가 없는 변수에는 부적합한 방법입니다.
from sklearn.preprocessing import LabelEncoder
# Label Encoding 적용
encoder = LabelEncoder()
X['Color'] = encoder.fit_transform(X['Color'])- 변환 방법 ② One-hot Encoding
- 각 범주를 0, 1의 조합으로 변환하는 방법으로, 위 예시의 경우 Red=[1,0,0,0], Blue=[0,1,0,0], Green=[0,0,1,0]..와 같이 변환할 수 있습니다.
- 위 예시의 '색상'처럼 순서가 없는 변수에 적합하지만, 범주 개수만큼 차원이 sparse하게 증가한다는 단점이 있다.
import pandas as pd
# One-Hot Encoding 적용 = 더미변수 추가하는 것과 동일!
X = pd.get_dummies(X, columns=['Color'])
# -------------- 변환 후 데이터 예시 -------------- #
# Color_Red Color_Blue Color_Green Color_Yellow
# 1 0 0 0
# 0 1 0 0
# 0 0 1 0
# 0 0 0 1
② 정보 이론에서의 '엔트로피'
- 정보 이론에서 엔트로피(Entropy)는 확률분포가 가지는 정보량(또는 확신도)을 수치로 표현한 것입니다. 이를 이해하기 위해서는 ‘정보량’이라는 개념을 먼저 이해할 필요가 있습니다. 정보량(I)이란 어떤 사건이 가지고 있는 정보의 양을 의미하는데, 통계학에서는 이를 다음과 같이 정의합니다.

- 여기서 $P(X)$는 특정 사건 X가 발생할 확률을 의미하고, 이 정보량의 추세를 그래프로 그려보면 위와 같은 꼴이 됩니다. 즉, 특정 사건이 발생할 확률이 작아질수록 정보량이 높은 것이라 보면 됩니다. 이는 다소 추상적이라 잘 와닿지 않을 수 있는데, '정보량'을 '놀람의 정도'라고 생각해보면 이해가 수월해집니다. 우리는 발생할 확률이 극히 적은 사건이 발생하면 굉장히 놀라기 마련인데, (ex. 8월에 눈이 오는 사건) 이렇게 '놀랄 정도'가 큰 것을 '정보량이 많다'고 이해하면 됩니다. 발생할 확률이 극히 적은 사건의 정보량은 그래프에서 보이듯 무한대에 가까워지겠죠.
- 엔트로피(Entropy)는 바로 이 정보량들의 평균을 의미합니다. 이는 다르게 말하면 '모든 사건의 정보량들의 기댓값'인데, 이를 수식으로 나타내면 아래와 같습니다. 이때 $n$은 사건의 종류(개수), $P(x_i)$는 i번째 사건의 발생확률을 의미합니다.
- 그래프를 보면 알 수 있듯이, 만약 어떤 사건의 발생확률이 (0.5, 0.5)처럼 비슷한 경우 엔트로피 값은 증가하게 됩니다. 반면 어떤 사건의 발생확률이 (0.1, 0.9)처럼 극명하게 차이나는 경우 엔트로피 값은 감소하게 됩니다.

- 자, 이제 $P(x_i)$라는 '발생확률'을 '영역 내 특정 클래스의 비율'이라고 생각하면, 불순도로 쓰이는 '엔트로피'의 개념을 이해할 수 있을 것입니다. 영역 내 클래스의 비율이 비슷하다면(=여러 클래스들이 골고루 있다면) 불순도(=Entropy)가 높다는 뜻이고, 이는 해당 영역을 특정 클래스로 규정짓기(분류하기) 힘들다는 뜻이겠죠!
③ RSS와 MSE 비교
| RSS | MSE | |
| 계산 식 |  |
 |
| 의미 | 잔차(residuals)의 제곱을 모두 합한 값 | RSS를 샘플 개수(자유도) n으로 나눈 값 |
| 특징 | • 절대적인 오차 크기를 나타내는 지표로, 샘플 수가 많아지면 RSS도 커짐 ⇒ 샘플 수가 다른 데이터셋끼리 비교가 어려움 • 회귀 트리의 분할 기준으로 사용됨 |
• 평균적인 오차 크기를 측정하는 지표로, 샘플 수(데이터 크기)에 영향을 받지 않음 ⇒ 여러 모델을 비교할 때 유용함 • 일반적인 회귀 모델의 성능을 평가/비교할 때 사용됨 |
| 비고 | 둘 다 오차의 단위가 제곱된 형태이므로 그대로 해석하긴 어려움. 그래서 원래 단위에 맞는 오차 크기를 직관적으로 알고 싶다면 RMSE(√MSE)를 사용하는 것이 적절함. |
|
🙏References
1) 의사결정나무 종류
2) 의사결정나무 학습 프로세스
'ML & DL > 데이터마이닝' 카테고리의 다른 글
| [데이터마이닝] 클러스터링 알고리즘 (0) | 2025.03.06 |
|---|---|
| [데이터마이닝] 앙상블 학습 (Ensemble learning) (0) | 2025.03.05 |
| [데이터마이닝] 트리 모델 가지치기(Pruning) (0) | 2025.03.04 |
| [데이터마이닝] 하이퍼파라미터 튜닝 (Grid search, Random search, Bayesian optimization) (0) | 2025.03.02 |
| [데이터마이닝] 지도학습의 기본 원리 (MSE Decomposition, Variance-Bias Trade off) (0) | 2025.03.01 |
