
1. 텐서(Tensor)란?
1.1. 벡터, 행렬, 텐서
- 딥러닝에서 다루는 가장 기본적인 단위 : 벡터, 행렬, 텐서
- 스칼라(scalar) : 단일한 값 1개
- 벡터(vector) : 1차원으로 구성된 값의 배열
- 행렬(matrix) : 2차원으로 구성된 값의 배열
- 텐서(tensor) : 3차원 이상의 배열
- 4차원 이상은 머리로 생각하기 어렵지만, 아래 그림처럼 그려볼 수는 있음
- 4d-tensor : 3d-tensor를 위로 쌓아 올린 모습
- 5d-tensor : 4d-tensor를 다시 옆으로 확장한 모습
- 6d-tensor : 5d-tensor를 다시 뒤로 확장한 모습

1.2. 텐서의 크기
- 딥러닝에서 행렬/텐서의 크기를 고려하는 것은 항상 중요함 ⇒ 2/3차원 텐서의 예시로 살펴보자
기본적인 2차원 텐서
- 전형적인 2차원 텐서의 크기 | t | = (batch size × dimension) 로 표현 가능

👨🏫 쉽게 설명하면...
인공지능을 학습시키기 위해서 준비한 훈련 데이터 하나의 크기를 256이라고 해봅시다. [3, 1, 2, 5, ...] 이런 숫자들의 나열이 256의 길이로 있다고 상상하면됩니다. 다시 말해 훈련 데이터 하나 = 벡터 하나에 숫자가 256개 있는 겁니다. 만약 이런 훈련 데이터의 개수가 3000개라고 한다면, 현재 전체 훈련 데이터의 크기는 3,000 × 256입니다. 행렬이니까 2D 텐서네요. 3,000개를 1개씩 꺼내서 처리하는 것도 가능하지만 컴퓨터는 훈련 데이터를 하나씩 처리하는 것보다 보통 덩어리로 처리합니다. 3,000개에서 64개씩 꺼내서 처리한다고 한다면 이 때 batch size를 64라고 합니다. 그렇다면 컴퓨터가 한 번에 처리하는 2D 텐서의 크기는 (batch size × dim) = 64 × 256입니다. 3,000을 64로 나누면 46.875가 나오는데요. 3,000개의 데이터를 64개씩 학습하면 총 47번 데이터를 넣어야 모든 데이터를 넣을 수 있겠군요!
* 출처: 유원준, 안상준 <딥러닝 파이토치 교과서 Wikidocs>
3차원 텐서 in CV
- Computer Vision 분야에서 다루는 이미지 데이터는 | t | = (batch size × width × height) 로 표현 가능
- 사진 한 장은 width * height 크기의 픽셀값들로 이루어져있음

3차원 텐서 in NLP
- Natural Language Processing 분야에서 다루는 이미지 데이터는 | t | = (batch size × length × dim) 로 표현 가능
- 문장 하나는 length * dim 크기의 배열 >>> length는 문장을 이루는 단어의 개수, dim은 각 단어의 임베딩 차원

👨🏫쉽게 설명하면...
아래와 같이 4개의 문장으로 구성된 전체 훈련 데이터가 있다고 합시다.
[[나는 사과를 좋아해], [나는 바나나를 좋아해], [나는 사과를 싫어해], [나는 바나나를 싫어해]]
컴퓨터는 아직 이 상태로는 '나는 사과를 좋아해'가 단어가 1개인지 3개인지 이해하지 못합니다. 컴퓨터의 입력으로 사용하기 위해서는 단어별로 나눠주어야 합니다.
[['나는', '사과를', '좋아해'], ['나는', '바나나를', '좋아해'], ['나는', '사과를', '싫어해'], ['나는', '바나나를', '싫어해']]
이제 훈련 데이터는 4 × 3의 크기를 가지는 2D 텐서입니다. 컴퓨터는 텍스트보다는 숫자를 더 잘 처리하기 때문에 각 단어를 벡터로 만들어줍니다. 아래처럼 각 단어를 3차원 벡터로 변환했다고 하겠습니다.
'나는' = [0.1, 0.2, 0.9]
'사과를' = [0.3, 0.5, 0.1]
'바나나를' = [0.3, 0.5, 0.2]
'좋아해' = [0.7, 0.6, 0.5]
'싫어해' = [0.5, 0.6, 0.7]
위 기준을 따라서 훈련 데이터를 재구성(벡터로 다시 표현)하면 아래와 같습니다. 이제 훈련 데이터는 4 × 3 × 3의 크기를 가지는 3D 텐서입니다.
[[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.7, 0.6, 0.5]], #나는 사과를 좋아해
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.7, 0.6, 0.5]], #나는 바나나를 좋아해
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.5, 0.6, 0.7]], #나는 사과를 싫어해
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.5, 0.6, 0.7]]] #나는 바나나를 싫어해
컴퓨터는 배치 단위로 가져가서 연산을 수행합니다. 예를 들어 batch size를 2라고 해보겠습니다. 그러면 각 배치의 텐서의 크기는 (2 × 3 × 3)입니다. 각각 (batch size, 문장 길이, 단어 벡터의 차원)으로 이해하면 됩니다.
Copy첫번째 배치 #1
[[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.7, 0.6, 0.5]],
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.7, 0.6, 0.5]]]
두번째 배치 #2
[[[0.1, 0.2, 0.9], [0.3, 0.5, 0.1], [0.5, 0.6, 0.7]],
[[0.1, 0.2, 0.9], [0.3, 0.5, 0.2], [0.5, 0.6, 0.7]]]
* 출처: 유원준, 안상준 <딥러닝 파이토치 교과서 Wikidocs>
2. 텐서 다뤄보기
2.1. Numpy
PyTorch로 텐서를 만들어보기 전에 먼저 익숙한 Numpy로 연습!
- 1) `np.array()`를 사용해 텐서 생성 (List를 넘파이 배열로 변환)
- `.ndim` : 배열의 차원을 반환
- `.shape` : 배열의 크기(형태)를 반환
- ❗(n, )는 (1, n)을 의미함. 예를 들어, (7, )은 배열의 크기가 (1 × 7)라는 뜻.

- 2) Indexing과Slicing으로 각 벡터의 원소에 접근 가능
- 인덱싱 : 특정 위치의 원소 접근
- 슬라이싱 : 특정 범위의 원소 접근 (마지막 원소는 제외함)

- 3) 다차원 array 생성 가능
- 리스트를 중첩하면 2, 3, 4, ... 차원의 다차원 행렬도 만들 수 있음

2.2. Pytorch
Numpy로도 3차원 텐서 만들 수는 있지만 비교를 위해 PyTorch로 넘어가자 (Pytorch is simillar to numpy, but it's better.)
1) 1차원 텐서
- `.FloatTensor` 로 텐서 생성
- `.dim()` : 배열의 차원을 반환
- `.shape` / `.size()` : 배열의 크기(형태)를 반환

- 역시 indexing과 slicing으로 원소 접근 가능

2) 2차원 텐서
- 역시 중첩 리스트로 입력하여 다차원 텐서 생성 가능

- 역시 indexing과 slicing으로 원소 접근 가능
- ⭐`[<첫 번째 차원의 선택 범위>, <두 번째 차원의 선택 범위>]`로 슬라이싱 = 각 범위도 슬라이싱 `[ : ]`으로 입력해야 함

3) 브로드캐스팅
- 기본적으로 두 행렬 A, B를 연산하려면, 크기가 맞아야 함
- 덧셈/뺄셈 : A, B 크기가 같아야 함
- 곱셈 : A의 마지막 차원과 B의 첫번째 차원이 같아야 함

- 하지만 딥러닝을 하다보면 크기가 다른 텐서끼리 연산을 수행할 경우가 생김
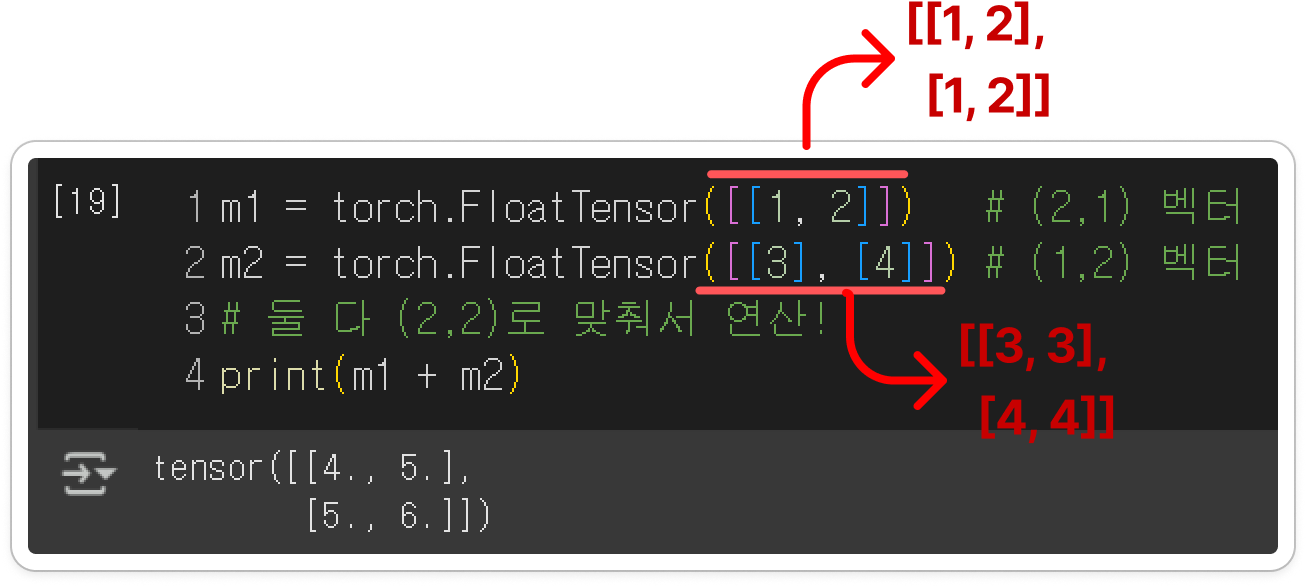
➡️이를 위해 Pytorch는 자동으로 크기를 맞춰서 연산을 수행하는 브로드캐스팅 기능을 제공함

3. Pytorch에서 자주 사용되는 기능
3.1. 행렬 곱셈과 곱셈 (Matmul, Mul)
- `.matmul` : 행렬 곱셈을 수행

- `.mul` : 원소별(element-wise) 곱셈을 수행 (그냥 `*` 곱셈기호로 연산해도 됨)
- ex) m2는 곱셈 연산 과정에서 브로드캐스팅 발생 = (2x2)크기로 바뀜 = m1의 각 열에 [1,2]가 곱해짐

3.2. 덧셈 (Sum)
- `.sum()` : 원소 전체의 덧셈을 수행

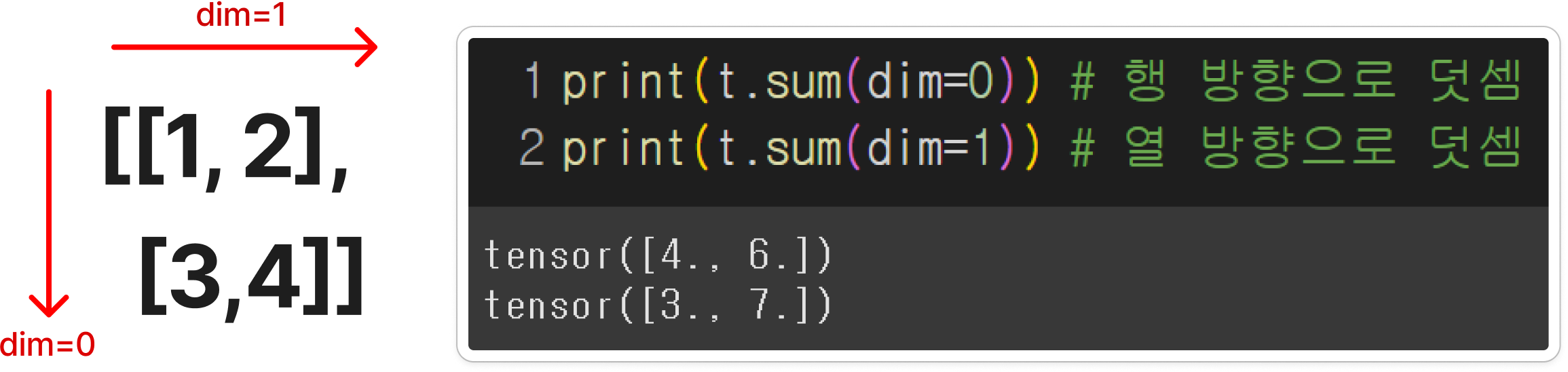
- `. sum (dim=)` : 차원(dim)을 인자로 주면, 그 차원의 방향으로 연산을 수행
- ⭐헷갈려서 3차원의 경우를 추가로 확인해 봄 (자세한 설명은 더보기 클릭!)

1) 연산 방향이 헷갈린다면 ⇒ 텐서의 대괄호 기준으로 생각하자!
- 0번째는 가장 바깥 대괄호, 1번째는 그 다음 ...
2) 연산 결과 shape이 헷갈린다면 ⇒ dim에 입력된 차원을 제거하면 됨!
- 위 예시의 경우, (2,3,2) 크기의 3차원 텐서임
- `t.sum(dim=1)`의 경우, 1번째 차원(=행)을 제거하면 (2,2)임
- 결과가 [[ 9, 12], [21, 21]] 이므로 크기 맞네! 🆗
👇아래 예시 하나씩 보면 이해될 거임..!



3.3. 평균 (Mean)
- `.mean()` : 전체 원소의 평균값을 반환

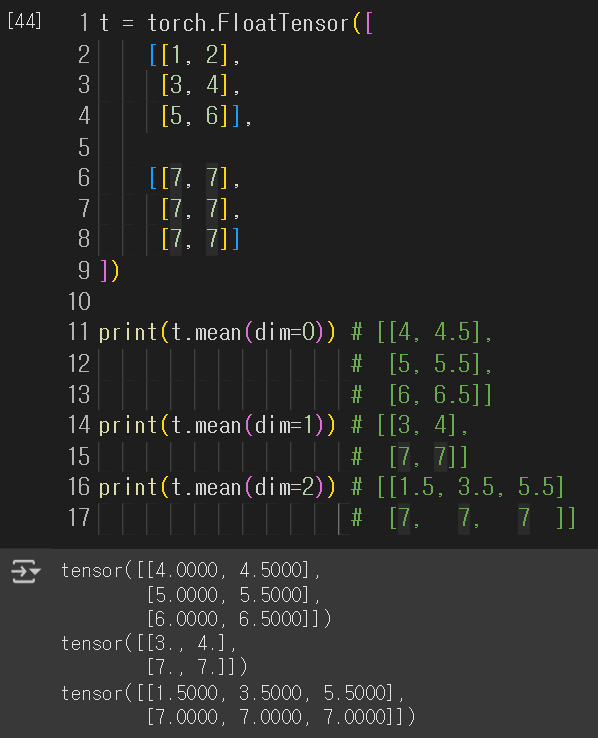
- `.mean(dim=)` : 마찬가지로 dim을 인자로 주면, 그 차원의 방향으로 연산을 수행

- 이번에도 3차원 추가 확인!
3.4. 최대(Max)와 아그맥스(ArgMax)
- `.max()` : 전체 원소 중 최댓값을 반환
- `. max (dim=)` : dim 차원의 관점에서 최댓값 들어있는 원소(이 원소는 값일 수도, 행일 수도, 배치일 수도 있는 것)를 반환
- 또한, argmax도 함께 반환해 줌! (같이 받고 싶지 않으면 `t.max(dim=1)[0]`으로 0번째 반환값만 선택하면 됨!)
- `.argmax()` : 최대값을 가진 인덱스를 반환

3.5. ⭐뷰(View)
- `.view()` : 텐서의 크기(Shape)를 변경해주는 역할 (=numpy의 `reshape`와 동일한 역할!!)
- ❗변경 전과 변경 후의 텐서 원소 개수는 유지되어야 함
- 특정 차원을 `-1`로 입력하면, 그 부분은 pytorch가 알아서 채워 넣음
- 예시1) 3차원 → 2차원 변환

- 예시2) 3차원 → 3차원 변환 (크기만 변환)

3.6. 스퀴즈(Squeeze)와 언스퀴즈(Unsqueeze)
- `.squeeze()` : 1인 차원을 제거하는 역할

- `.unsqueeze()` : 특정 위치에 1인 차원을 추가하는 역할 (squeeze의 정반대)
- 참고로, `view`로도 같은 작업을 할 수 있음 (view, squeeze, unsqueeze는 모두 텐서의 원소 수를 그대로 유지하면서 모양과 차원을 조절하는 기능)


3.7. 타입 캐스팅(Type Casting)
- 텐서에는 다양한 자료형이 있음 (데이터마다 다름)
- ex) `torch.FloatTensor` : 32비트의 부동 소수점, `torch.LongTensor` : 64비트의 부호 있는 정수
- `torch.cuda.FloatTensor` 처럼 GPU 연산을 위한 자료형도 있음

- 이 자료형을 변환하는 것을 타입 캐스팅이라고 함
- `.float()` : Float 타입으로 변환
- `.long()` : Long 타입으로 변환

3.8. 연결(Concatenate)
- 딥러닝에서는 모델의 입력 또는 중간 연산에서 텐서들을 연결하는 경우가 많음. ⇒ 두 가지의 정보를 모두 사용한다는 의미!
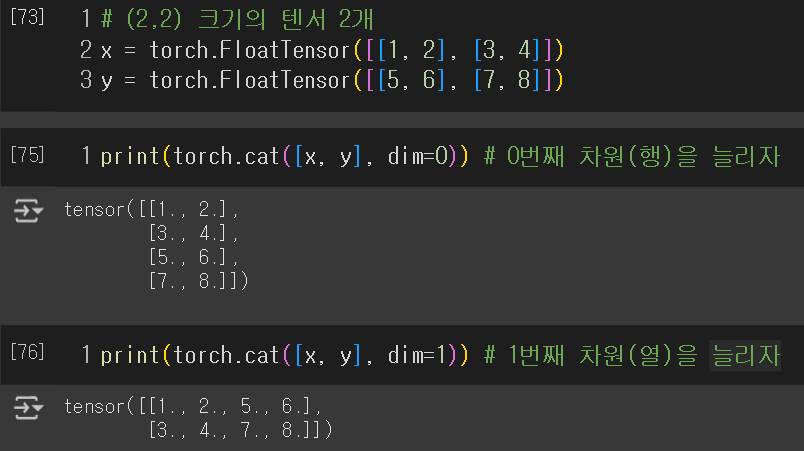
- `.cat()` : 여러 텐서들을 연결함 ⭐`dim` 인자로 '연결하면서 어느 차원을 늘릴지' 설정 가능!
3.9. 스택킹(Stacking)
- 여러 텐서들을 연결할 때, `.stack()`을 사용할 수도 있음
- `.cat()`보다 많은 연산을 포함하고 있어서 더 편리할 때가 있음! (아래 예시 참고)

- stacking 역시 `dim` 인자를 입력해서 방향 설정 가능!

3.10. ones_like와 zeros_like
- `.ones_like(x)` : x와 동일한 크기지만 값이 1로만 채워진 텐서를 생성
- `.zeros_like(x)` : x와 동일한 크기지만 값이 0으로만 채워진 텐서를 생성

3.11. 덮어쓰기 연산(In-place Operation)
- 연산 코드 뒤에 underscore (`_`)를 붙이면, 해당 연산 값을 변수에 저장(업데이트) 해줌!
- ex) `mul_` : 곱셈 연산 수행 + 저장

🙏References
- 유원준, 안상준 님의 <딥러닝 파이토치 교과서 Wikidocs> (https://wikidocs.net/book/2788) 를 공부하고 정리한 내용입니다.
'ML & DL > 딥러닝 기초' 카테고리의 다른 글
| [Pytorch+딥러닝] 3-4. 미니 배치와 데이터 로더 (0) | 2025.02.20 |
|---|---|
| [Pytorch+딥러닝] 3-3. nn.Module과 클래스로 구현하기 (1) | 2025.02.19 |
| [Pytorch+딥러닝] 3-2. 다중 선형 회귀 (0) | 2025.02.18 |
| [Pytorch+딥러닝] 3-1. 선형 회귀와 자동 미분 (0) | 2025.02.17 |
| [Keras] Sequential API vs. Functional API 비교 (0) | 2025.02.03 |